Kinematic description
The coordinate system used with both families of elements is the cylindrical system (r, z, θ), where r measures the distance of a point from the axis of the cylindrical system, z measures its position along this axis, and θ measures the angle between the plane containing the point and the axis of the coordinate system and some fixed reference plane that contains the coordinate system axis. The order in which the coordinates and displacements are taken in these elements is based on the convention that z is the second coordinate. This order is not the same as that used in three-dimensional elements in Abaqus, in which z is the third coordinate, nor is it the order (r, θ, z), usually taken in cylindrical systems.
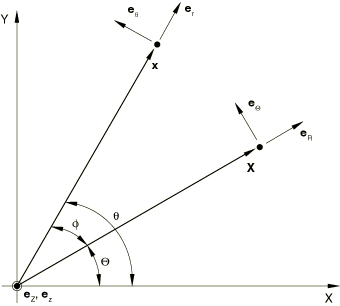
Let eR, eZ, and eΘ be unit vectors in the radial, axial, and circumferential directions at a point in the undeformed state, as shown in Figure 1.
The reference position X of the point can be represented in terms of the original radius R and the axial position Z:
Likewise, let er, ez, and eθ be unit vectors in the radial, axial, and circumferential directions at a point in the deformed state. As shown in Figure 1, the radial and circumferential base vectors depend on the θ coordinate: er=er(θ) and eθ=eθ(θ). The current position x of the point can be represented in terms of the current radius r and the current axial position z:
The general axisymmetric motion at a point can be described by
As the above description implies, the degrees of freedom ur, uz, and ϕ are independent of Θ. Moreover, the reference cross-section of interest is at Θ=0, but for the benefit of the mathematical analysis to follow it is important that Θ be nonzero in the above expression for θ.