Stress wave propagation illustrated

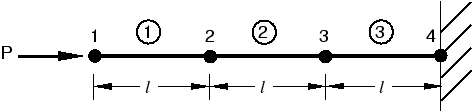
This section attempts to provide some conceptual understanding of how forces propagate through a model when using the explicit dynamics method. In this illustrative example we consider the propagation of a stress wave along a rod modeled with three elements, as shown in Figure 1. We will study the state of the rod as we increment through time.

Figure 1. Initial configuration of a rod with a concentrated load, P, at the free end.

In the first time increment node 1 has an acceleration, u¨1, as a result of the concentrated force, P, applied to it. The acceleration causes node 1 to have a velocity, u˙1, which, in turn, causes a strain rate, ε˙e⁢l⁢1, in element 1. The increment of strain, Δ⁢εe⁢l⁢1, in element 1 is obtained by integrating the strain rate through the time of increment 1. The total strain, εe⁢l⁢1, is the sum of the initial strain, ε0, and the increment in strain. In this case the initial strain is zero. Once the element strain has been calculated, the element stress, σe⁢l⁢1, is obtained by applying the material constitutive model. For a linear elastic material the stress is simply the elastic modulus times the total strain. This process is shown in Figure 2. Nodes 2 and 3 do not move in the first increment since no force is applied to them.

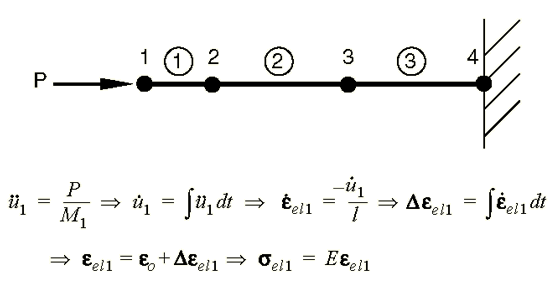
Figure 2. Configuration at the end of increment 1 of a rod with a concentrated load, P, at the free end.

In the second increment the stresses in element 1 apply internal, element forces to the nodes associated with element 1, as shown in Figure 3. These element stresses are then used to calculate dynamic equilibrium at nodes 1 and 2.

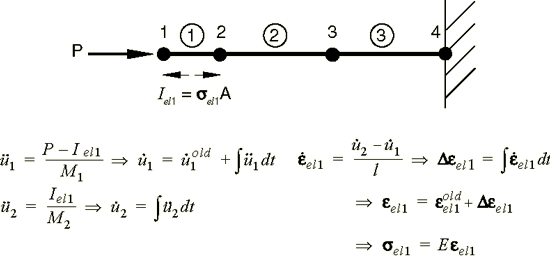
Figure 3. Configuration of the rod at the beginning of increment 2.

The process continues so that at the start of the third increment there are stresses in both elements 1 and 2, and there are forces at nodes 1, 2, and 3, as shown in Figure 4. The process continues until the analysis reaches the desired total time.

Figure 4. Configuration of the rod at the beginning of increment 3.