Damage Evolution for Fiber-Reinforced Composites Using Multiscale Modeling

You can specify damage evolution for fiber-reinforced materials using multiscale modeling.

The damage evolution capability for multiscale fiber-reinforced materials in Abaqus/Standard:

assumes that damage is characterized by progressive degradation of the material stiffness, leading to material failure;
models the degradation of the composite at the constituent level, leading to composite-level failure through homogenization;
requires the undamaged response of the material to be linear elastic (see Linear Elastic Behavior);
offers options to model energy dissipation in each constituent during the damage process in a unidirectional fiber-reinforced composite;
offers options to model instantaneous degradation of material stiffness with user-specified scaling factors (this method is the only option for modeling the progressive damage of a woven composite); and
can be used in combination with a viscous regularization scheme to improve the convergence rate in the softening regime.

This page discusses:

Damage Evolution
Maximum Degradation
Viscous Regularization
Elements
Output

Damage Evolution

Damage Initiation for Fiber-Reinforced Composites Using Multiscale Modeling discussed the constituent-level damage initiation in fiber-reinforced composites. This section discusses the post-damage initiation behavior for cases in which a damage evolution model has been specified. The damage evolution is modeled at the constituent level, leading to the damage process of a composite through homogenization. Prior to damage initiation, the constituent material is linearly elastic, with the stiffness matrix of an isotropic or a transversely isotropic material. Thereafter, the response of the constituent material is computed from

σ = C_{d} ε^{e l},

where

ε^{e l}

is the elastic strain, and

C_{d}

is the damaged elasticity matrix, which has the form

C_{d} = (1 - D) C,

where

D

is the damage variable and

C

is the undamaged stiffness matrix of the constituent.

The damage variables, $D$ , are derived from damage variables in each constituent based on tension or compression modes, as follows:

Fiber:: $\begin{matrix} D & = {\begin{matrix} d_{f}^{t} & if {\hat{σ}}_{11} \geq 0, \\ d_{f}^{c} & if {\hat{σ}}_{11} < 0. \end{matrix} \end{matrix}$
Matrix:: $\begin{matrix} D & = {\begin{matrix} d_{m}^{t} & if {\hat{σ}}_{22} + {\hat{σ}}_{33} \geq 0, \\ d_{m}^{c} & if {\hat{σ}}_{22} + {\hat{σ}}_{33} < 0 . \end{matrix} \end{matrix}$

{\hat{σ}}_{11}

{\hat{σ}}_{22}

, and

{\hat{σ}}_{33}

are components of the effective stress tensor at the constituent level.

Evolution of Damage Variables for Each Mode

To alleviate mesh dependency during material softening, Abaqus introduces a characteristic length into the formulation so that the constitutive law is expressed in a stress-displacement relation. The damage variable evolves such that the stress-displacement behaves as shown in Figure 1 in each of the two failure modes (tension and compression). The positive slope of the stress-displacement curve before damage initiation corresponds to linear elastic material behavior; the negative slope after damage initiation is achieved by evolution of the respective damage variables according to the equations shown below.

The equivalent displacement and stress for the tension and compression damage modes are defined as follows:

Tension $({\hat{σ}}_{11} \geq 0)$ with the HSNFIBER damage criterion:

δ_{e q}^{f t} = L^{c} \sqrt{{⟨ ε_{11} ⟩}^{2} + α (ε_{12}^{2} + ε_{13}^{2})},

σ_{e q}^{f t} = \frac{⟨ σ_{11} ⟩ ⟨ ε_{11} ⟩ + α (τ_{12} ε_{12} + τ_{13} ε_{13})}{δ_{e q}^{f t} / L^{c}},

Compression $({\hat{σ}}_{11} < 0)$ with the HSNFIBER damage criterion:

δ_{e q}^{f c} = L^{c} \sqrt{{⟨ {- ε}_{11} ⟩}^{2} + α (ε_{12}^{2} + ε_{13}^{2})},

σ_{e q}^{f c} = \frac{⟨ {- σ}_{11} ⟩ ⟨ {- ε}_{11} ⟩ + α (τ_{12} ε_{12} + τ_{13} ε_{13})}{δ_{e q}^{f t} / L^{c}},

Tension $({\hat{σ}}_{22} + {\hat{σ}}_{33} \geq 0)$ with the HSNMATRIX or TSINVMATRIX damage criterion:

δ_{e q}^{m t} = L^{c} \sqrt{{⟨ I_{t, ε} ⟩}^{2} + ε_{12}^{2} + ε_{13}^{2}},

σ_{e q}^{m t} = \frac{⟨ I_{t} ⟩ ⟨ I_{t, ε} ⟩ + τ_{12} ε_{12} + τ_{13} ε_{13}}{δ_{e q}^{m t} / L^{c}} .

where $I_{t} = \frac{{\hat{σ}}_{22} + {\hat{σ}}_{33}}{2} + {[{(\frac{{\hat{σ}}_{22} - {\hat{σ}}_{33}}{2})}^{2} + {({\hat{σ}}_{23})}^{2}]}^{2}$ and $I_{t, ε} = \frac{{\hat{ε}}_{22} + {\hat{ε}}_{33}}{2} + {[{(\frac{{\hat{ε}}_{22} - {\hat{ε}}_{33}}{2})}^{2} + {({\hat{ε}}_{23})}^{2}]}^{2}$ are the maximum principal stress/strain in the plane normal to the fiber direction.

Compression $({\hat{σ}}_{22} + {\hat{σ}}_{33} < 0)$ with the HSNMATRIX or TSINVMATRIX damage criterion:

δ_{e q}^{m c} = L^{c} \sqrt{{⟨ I_{c, ε} ⟩}^{2} + ε_{12}^{2} + ε_{13}^{2}},

σ_{e q}^{m c} = \frac{⟨ I_{c} ⟩ ⟨ I_{c, ε} ⟩ + τ_{12} ε_{12} + τ_{13} ε_{13}}{δ_{e q}^{m t} / L^{c}} .

where $I_{c} = \frac{{\hat{σ}}_{22} + {\hat{σ}}_{33}}{2} - {[{(\frac{{\hat{σ}}_{22} - {\hat{σ}}_{33}}{2})}^{2} + {({\hat{σ}}_{23})}^{2}]}^{2}$ and $I_{c, ε} = \frac{{\hat{ε}}_{22} + {\hat{ε}}_{33}}{2} - {[{(\frac{{\hat{ε}}_{22} - {\hat{ε}}_{33}}{2})}^{2} + {({\hat{ε}}_{23})}^{2}]}^{2}$ are the minimum principal stress/strain in the plane normal to the fiber direction.

The characteristic length, $L^{c}$ , is based on the element geometry and formulation. $L^{c}$ is a typical length of a line across an element for a first-order element and half of the same typical length for a second-order element. For membranes and shells, $L^{c}$ is a characteristic length in the reference surface, computed as the square root of the area. The symbol $⟨ ⟩$ in the equations above represents the Macaulay bracket operator, which is defined for every $α \in ℜ$ as $⟨ α ⟩ = (α + | α |) / 2$ .

After damage initiation (that is, $δ_{e q} \geq δ_{e q}^{0}$ ) for the behavior shown in Figure 1, the damage variable for a particular mode is given by the following expression:

d = \frac{δ_{e q}^{f} (δ_{e q} - δ_{e q}^{0})}{δ_{e q} (δ_{e q}^{f} - δ_{e q}^{0})},

where

δ_{e q}^{0}

is the initial equivalent displacement at which the initiation criterion for that mode was met, and

δ_{e q}^{f}

is the displacement at which the material is completely damaged in this failure mode. The relation above is presented graphically in Figure 2.

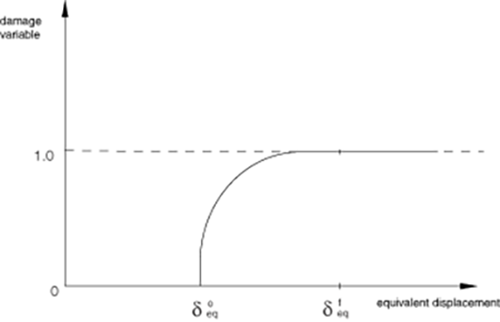
The values of $δ_{e q}^{0}$ for the various modes depend on the elastic stiffness and the strength parameters specified as part of the damage initiation definition (see Damage Initiation for Fiber-Reinforced Composites). For each failure mode, you must specify the energy dissipated by failure, $G^{c}$ , which corresponds to the area of the triangle OAC in Figure 3.

The values of $δ_{e q}^{f}$ for the various modes depend on the respective $G^{c}$ values.

Unloading from a partially damaged state, such as point B in Figure 3, occurs along a linear path toward the origin in the plot of equivalent stress versus equivalent displacement. This same path is followed back to point B on reloading as shown in the figure.

Input File Usage

Use the following option to define the damage evolution law:

DAMAGE EVOLUTION, TYPE=ENERGY, SOFTENING=LINEAR
 $G_{t}^{c}$ ,  $G_{c}^{c}$

where $G_{t}^{c}$ , $G_{c}^{c}$ are energies dissipated during damage for tension and compression failure modes, respectively.

You can specify the post-damage residual stiffness scaling factor directly for the tension and compression failure modes. The scaling factor is related to the damage variable as

S F = 1 - D .

When a small scaling factor is specified at the onset of damage initiation, the sudden stiffness degradation often leads to convergence difficulties in implicit analyses. Discontinuous solutions also require a larger number of iterations to reach convergence (see Commonly Used Control Parameters for information about how to modify solution control parameters to achieve better convergence). You can also use the viscous regularization scheme described below (Viscous Regularization) to overcome these difficulties.

Input File Usage

Use the following option to define the post-damage residual stiffness scaling factor directly for damage evolution:

DAMAGE EVOLUTION, TYPE=DISCONTINUOUS
 ${S F}_{t}$ ,  ${S F}_{c}$

where ${S F}_{t}$ and ${S F}_{c}$ are the post-damage scaling factor for tension and compression failure modes, respectively.

Maximum Degradation

When a fracture energy is specified for damage evolution, Abaqus/Standard limits the damage variable at a constituent to a maximum value of 0.99 in both tension and failure modes. You can modify this upper bound as discussed in Controlling Element Deletion and Maximum Degradation for Materials with Damage Evolution.

Abaqus/Standard does not delete elements after failure with this multiscale damage model.

Viscous Regularization

Material models exhibiting softening behavior and stiffness degradation often lead to severe convergence difficulties in implicit analysis programs such as Abaqus/Standard. You can overcome some of these convergence difficulties using the viscous regularization scheme, which slows down the rate of increase of damage.

In this regularization scheme, a viscous damage variable is defined by the evolution equation:

{\dot{d}}_{v} = \frac{1}{η} (d - d_{v}),

where $η$ is the viscosity coefficient representing the relaxation time of the viscous system, and d is the damage variable evaluated in the inviscid backbone model. The damaged response of the viscous material is given as

σ = C_{d} ϵ,

where the damaged elasticity matrix, $C_{d}$ , is computed using viscous values of damage variables. Using viscous regularization with a small value of the viscosity parameter (small compared to the characteristic time increment) usually helps improve the rate of convergence of the model in the softening regime without compromising results. The basic idea is that the solution of the viscous system relaxes to that of the inviscid case as $t / η \to \infty$ , where t represents time.

In Abaqus/Standard, the approximate amount of energy associated with viscous regularization over the whole model or over an element set is available using the output variable ALLCD.

Defining Viscous Regularization Coefficients

You can specify different values of viscous coefficients for different failure modes.

Input File Usage

Use the following option to define viscous coefficients:

DAMAGE STABILIZATION
  $η_{t}$ ,  $η_{c}$

where $η_{t}$ and $η_{c}$ are viscosity coefficients for tension and compression failure modes, respectively.

Elements

The multiscale damage model can be used with any elements in Abaqus/Standard that include mechanical behavior; that is, elements that have displacement degrees of freedom.

Output

In addition to the standard output identifiers available in Abaqus/Standard (Abaqus/Standard Output Variable Identifiers), the following variables relate specifically to damage evolution in the multiscale fiber-reinforced composite damage model (the integration point output variables are available only when you request micro-level output in your output request):

DAMAGEFT: Fiber tensile damage variable when the HSNFIBER damage criterion is specified.
DAMAGEFC: Fiber compressive damage variable when the HSNFIBER damage criterion is specified.
DAMAGEMT: Matrix tensile damage variable when the HSNMATRIX or TSINVMATRIX damage criterion is specified.
DAMAGEMC: Matrix compressive damage variable when the HSNMATRIX or TSINVMATRIX damage criterion is specified.
EDMDDEN: Energy dissipated per unit volume in the element by damage.
ELDMD: Total energy dissipated in the element by damage.
DMENER: Energy dissipated per unit volume by damage.
ALLDMD: Energy dissipated in the whole (or partial) model by damage.
ECDDEN: Energy per unit volume in the element that is associated with viscous regularization.
ELCD: Total energy in the element that is associated with viscous regularization.
CENER: Energy per unit volume that is associated with viscous regularization.
ALLCD: The approximate amount of energy over the whole model or over an element set that is associated with viscous regularization.