Minimizing the Compliance of the Bonnet Model

This example shows the difference between a MIN and MINMAX formulation for the Objective Function.

See Also
About Checking the Quality of the Optimization Result
  1. Define three Design Responses (DRESP) with the compliance of each load case: 
    DRESP
  ID_NAME    = COMPL_1
  TYPE       = STRAIN_ENERGY
  DEF_TYPE   = SYS
  LC_SET     = STATIC,1,
  EL_GROUP   = ALL_ELEMENTS
  GROUP_OPER = SUM
END_

    DRESP
  ID_NAME    = COMPL_2
  TYPE       = STRAIN_ENERGY
  DEF_TYPE   = SYS
  LC_SET     = STATIC,2,
  EL_GROUP   = ALL_ELEMENTS
  GROUP_OPER = SUM
END_

    DRESP
  ID_NAME    = COMPL_3
  TYPE       = STRAIN_ENERGY
  DEF_TYPE   = SYS
  LC_SET     = STATIC,3,
  EL_GROUP   = ALL_ELEMENTS
  GROUP_OPER = SUM
END_
  2. Define the Objective Function (OBJ_FUNC) with a MIN formulation: 
    OBJ_FUNC
  ID_NAME = MIN_COMP
  DRESP   = COMPL_1, 1.0, 0.0
  DRESP   = COMPL_2, 1.0, 0.0
  DRESP   = COMPL_3, 1.0, 0.0
  TARGET  = MIN
END_

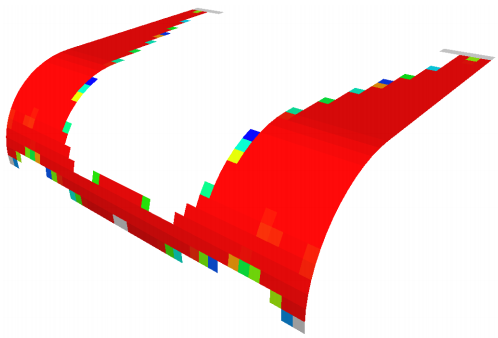
    The formulation of the optimization problem is done in the classic way, which means that the compliance of all three load cases is added and the sum of the compliance of the three load cases is minimized. The result looks as follows:



  3. Define the Objective Function (OBJ_FUNC) with a MINMAX formulation: 
    OBJ_FUNC
  ID_NAME = MIN_MAX_COMP
  DRESP   = COMPL_1, 1.0, 0.0
  DRESP   = COMPL_2, 1.0, 0.0
  DRESP   = COMPL_3, 1.0, 0.0
  TARGET  = MIN_MAX
END_

    In this case, the sum of the compliance is not minimized. Instead the maximum compliance of the three defined design responses is minimized. As result the optimization system ends up with the following structure: