Exponential Distribution

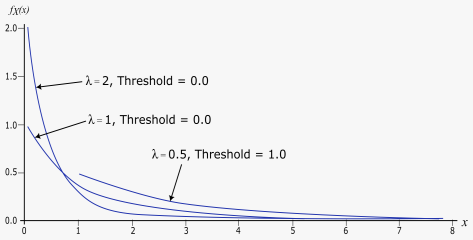
The exponential probability density function for a random variable $X$ is given by

$f_{X} (x) = λ \exp (- λ (x - t)); λ > 0, t \geq 0$

where the parameter $λ$ is a scale parameter. The exponential distribution function is

$F_{X} (x) = 1 - \exp (- λ (x - t)); λ > 0, t \geq 0$

The mean value and standard deviation of the random variable $X$ for the exponential distribution are given by

$μ_{X} = σ_{X} = \frac{1}{λ} + t; λ > 0, t \geq 0$

The exponential probability density function, as shown in the following figure, is often used to describe usage life of components.