Overview of Stress in Topology Optimization

$SIG_TOPO_MISES = \max | \frac{{(σ_{vMises})}^{2}}{{(f (ρ_{i}) σ_{y})}^{2}} \cdot σ_{y} |$

The $σ_{v M i s e s}$ is the elemental centroidal von Mises stress, $σ_{y}$ is the reference stress and $f (ρ_{i})$ is a factor for interpolating the stresses of the elements having intermediate densities (given by the topology optimization, see Stress Interpolation).

Only von Mises stress can be applied in topology optimization.

Analysis Types: Static Linear and Non-Linear (Contact) Analysis

Geometrical and material nonlinearities in element group are not supported.


$({4 π}^{2} f^{2} M - K) φ = 0$

For weighted centroidal von Mises stress for topology optimization, the following table shows the allowed combinations between strategy and the items OBJ_FUNC and CONSTRAINT with C for controller and S for sensitivity-based optimization.


	TOPO	SHAPE	BEAD	SIZING
OBJ_FUNC	S
CONSTRAINT	S

Note:

Stress applied in topology optimization cannot directly be compared to the von Mises stress given as output from the finite element solver. Only for solid elements ( $ρ = 1$ ) the von Mises stresses given by Tosca Structure stresses is equal to the von Mises stresses as output from the FE-solver (see Stress Interpolation).

Stress Calculation

The von Mises stress is calculated in the elemental centroid for avoiding stress singularities that might be present in the initial model or appear in the nonsmoothed topology optimized structures. This is also shown in the following figure:

Reference Stress for Objective Function

The reference stress $σ_{r e f}$ is defined in the objective function command or will be automatically calculated by Tosca Structure for the objective function.

A reference stress for the objective function terms can be directly defined as


OBJ_FUNC
  ID_NAME = OBJ_FUNCTION_ID
  DRESP   = DRESP_ID_1,<weight_fact_1>, <ref_stress_1>
  DRESP   = DRESP_ID_2,<weight_fact_2>, <ref_stress_2>
  ...
  TARGET  = MIN
END_

where <reference stress 1> and <reference stress 2> correspond to $σ_{r e f}$ . The reference stress values should not be chosen too low as this might cause numerical singularities. This corresponds to


$\min {α_{1} \max \| \frac{{(σ_{vMises})}^{2}}{{(f (ρ_{i}) σ_{{ref}_{1}})}^{2}} \| + α_{2} \max \| \frac{{(σ_{vMises})}^{2}}{{(f (ρ_{i}) σ_{{ref}_{2}})}^{2}} \|}$

If the user does not define a reference stress in the objective function command, Tosca Structure automatically determines a reference stress that is generated in the initial optimization iteration and is written to TOSCA.OUT.

Constraint Value

A limitation on the stresses can be formed for a DRESP of type SIG_TOPO_MISES used in a constraint definition with the LE_VALUE parameter:


CONSTRAINT
  ID_NAME   = STRESS_CONSTRAINT
  DRESP     = DRESP_STRESS_ID
  MAGNITUDE = ABS
  LE_VALUE  = <stress_constraint>
END_

This corresponds to restricting the weighted centroidal von Mises stress by the constraint value stress_constraint= $σ_{c o n}$ :


$\max \| \frac{{(σ_{vMises})}^{2}}{{(f (ρ_{i}) σ_{con})}^{2}} \cdot σ_{con} \| \leq σ_{con}$

Important:

$σ_{ref}$ is equal to the reference value when the DRESP defined by SIG_TOPO_MISES is applied in the objective function. The reference stress $σ_{ref}$ can be changed by modifying the reference value in the objective.
$σ_{con}$ is equal to LE_VALUE (or GE_VALUE) when the DRESP defined by SIG_TOPO_MISES is applied in a constraint.
A DRESP being TYPE = SIG_TOPO_MISES can only be applied once in the objective function or as constraint.
A reference stress or constrained stress which is too low might cause numerical singularities.

Stress Interpolation

The factor $f (ρ_{i})$ describes a function for the interpolation of stresses depending of the density $ρ_{i}$ of the element i.

The interpolation is needed because during the topology optimization the densities of the elements are modified and can have a minimum value close to zero. Stress values calculated by the solver for transition or soft elements (that is, elements with low density) have no real physical meaning for the stresses and must be weighted by a factor to allow for a successful optimization convergence.

The following figure shows the densities of elements during the optimization: On the left, the initial equal density of all elements can be seen, at the top there are the modified densities during the topology optimization iterations and on the right the final density values for the optimized model.

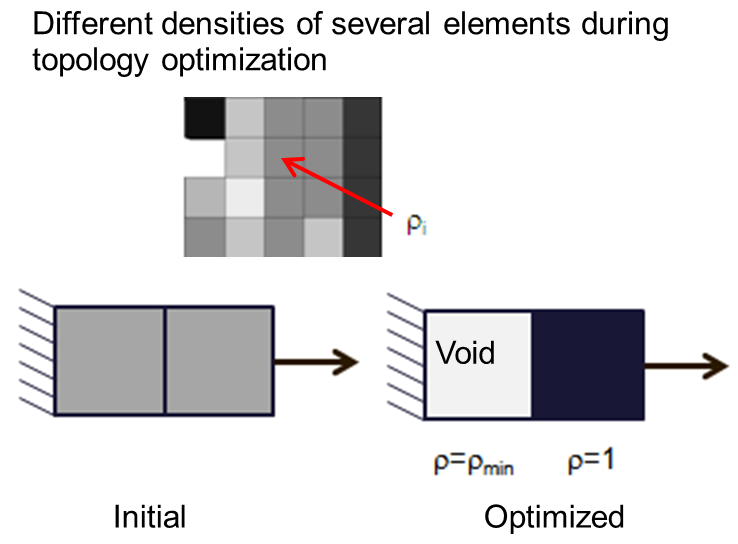The stress interpolation for intermediate densities is similar to the stiffness material interpolation and can be illustrated as

Thus, the stress measure SIG_TOPO_MISES applied in topology optimization cannot be directly compared to the von Mises stresses seen as output from the finite element solver. Only for solid elements ( $ρ = 1$ ) and with an active stress constraint the SIG_TOPO_MISES corresponds to the von Mises stresses calculated by the FE-solver.


Solid elements:	$f (ρ_{i} = 1) = 1 \Rightarrow \frac{{(σ_{vMises})}^{2}}{{(f (ρ_{i}) σ_{y})}^{2}} = \frac{{σ_{vMises}}^{2}}{σ_{y}^{2}}$
Von Mises stress = constraint stress:	$\frac{{σ_{vMises}}^{2}}{σ_{con}^{2}} = 1 \Rightarrow DRESP = σ_{vMises} = σ_{con}$

Element Group

The element group for the stress measure can consist of both design and nondesign elements.

Frequently, the initial model for the optimization contains nonphysical modeling around loaded nodes and boundary conditions, respectively. The user should avoid including stresses from stress singularities caused by external loaded nodes or by boundary conditions, as shown in the following figure. These singularities are eliminated by excluding these elements from the group used for calculating the DRESP.

Supported Element Types

Supported element types are 3D standard continuum elements:

Hexahedral 8 and 20 node elements
Tetrahedral 4 (not recommended) and 10 node elements
Pentahedron 6 and 15 nodes elements

All linear isotropic materials are supported for the elements in the element group. Anisotropic and nonlinear materials both inside and outside the design domain (DV_TOPO) are only supported if the stresses of these materials are not a part of the element group applied for calculation of the DRESP of TYPE = SIG_TOPO_MISES.

Note: Pyramidal 5 and 13 node elements as well as shell elements are not supported.

Important: Shear and volume locking in the finite element yield wrong results not only in the finite element analysis but can also cause optimization convergence problems when such stress responses are included in the optimization formulation. Especially, the linear 4 node tetrahedral elements should be avoided. Instead it is recommended to use the quadratic10 node tetrahedral element or the linear 8 node hexahedral element.

Load Cases

Several load cases can be defined for the stress measure.

Static linear analysis is supported. For static nonlinear analysis, only contact is supported.

Thus, geometric nonlinearities (like large deformation) and nonlinear materials are not supported.