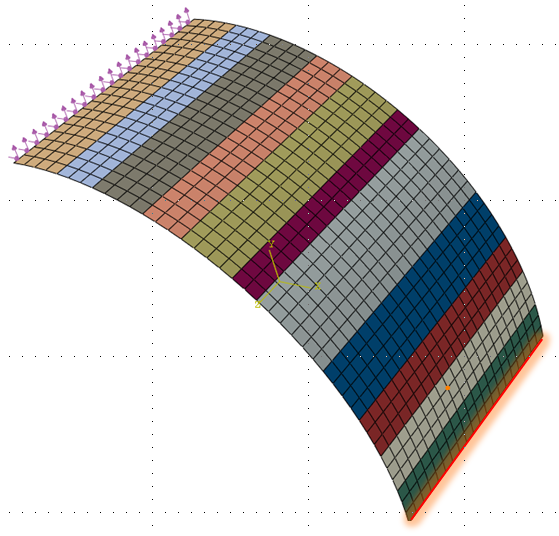
FE Model
The model is a curved shell fixed at one edge and loaded in the X and Y
directions on the opposite edge. To obtain mechanically sensible results
from the optimization, the elements are clustered into 11 groups. Thickness
of each group will correspond to one design variable.
| FE Model |
Clustering |

|
|
Optimization Problem
We consider a basic compliance minimization problem with a volume constraint.
The *.par file is shown below.
DVCON_SIZING
ID_NAME = DVCON_SIZING_set_discr
EL_GROUP = ALL_ELEMENTS
CHECK_TYPE = DISCRETE
DISCR_LIST_FILE = Sheet_sizing.csv
DISCR_CYCLE = 10
DISCR_INTERVAL = 4
DISCR_FRACTION = 0.2
DISCR_CHANGE = 10
END_
DVCON_SIZING
ID_NAME = DVCON_SIZING_bounds
EL_GROUP = ALL_ELEMENTS
CHECK_TYPE = THICKNESS_BOUNDS
MAGNITUDE = ABS
LOWER_BOUND = 0.1
UPPER_BOUND = 2.0
END_
. . .
OPT_PARAM
STOP_CRITERION_ITER = 30
END_
Optimization Results
The following table contains the discrete thickness values which
were available for the considered optimization.
| Available thicknesses: |
| 0.152;0.163;0.170;0.191;0.208;0.229;0.246;0.267;0.305;0.343;0.378;0.417 |
| 0.455;0.531;0.607;0.683;0.759;0.836;0.912;1.062;1.214;1.367;1.519;1.709 |
| 1.897;2.278;2.657;3.038;3.416;3.797;4.176;4.554;4.935;5.314;5.695;6.073 |
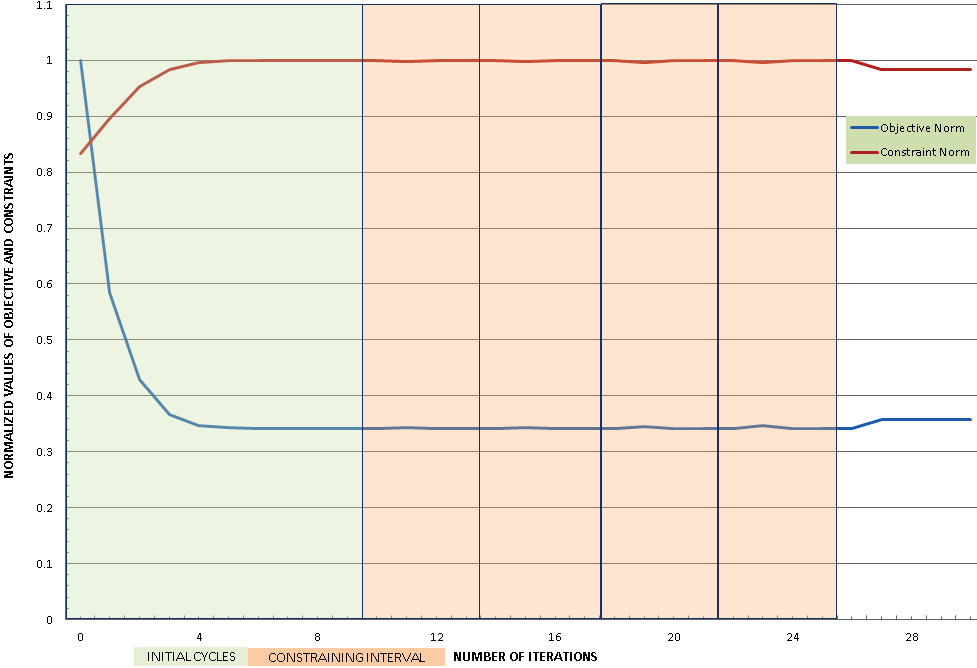
The figure below shows the optimization history of objective and constraints. The constraining cycles and the initial cycles have been marked out.
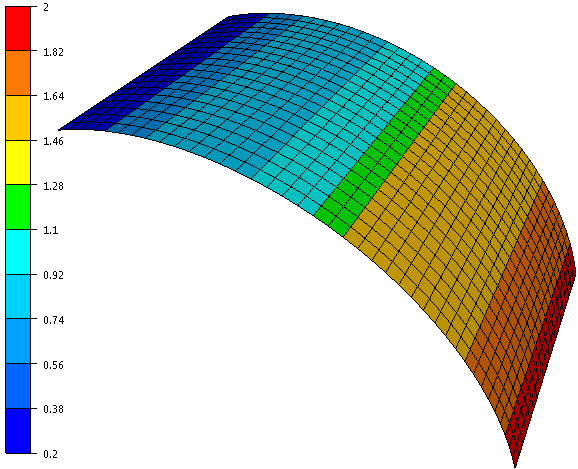
| Optimized discrete thicknesses: |
| 0.3780;0.6070;0.7590;0.9120;1.0620;1.2140;1.5190;1.5190;1.7090;1.7090;1.8970 |
| Resulting thicknesses using sizing optimization with discrete design variables |
|
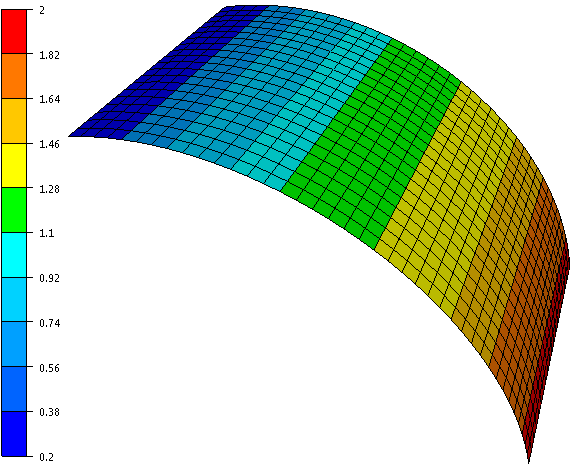
| Optimized continuous thicknesses: |
| 0.3795; 0.5878;0.7792;0.9563;1.1177;1.2414;1.4012;1.5763;1.6843;1.7651;1.8386 |
| Resulting thicknesses using sizing optimization with continuous design variables |
|
The difference in the objective functions for the standard and discrete
optimization is less than 2% and the constraints are fulfilled within an
error of 0.001 in this example.