Maximizing the Torsional Modal Eigenfrequency

Often it is needed to increase a specific eigenfrequency in the eigenfrequency spectrum belonging to a certain eigenmode. In this case, a specific eigenfrequency is defined using TYPE = DYN_FREQ.

This page discusses:

See Also
Overview of Eigenfrequency

Formulation of the Optimization Problem

The optimization task is to maximize the second torsional modal eigenfrequency with a volume constraint of 100% and without any boundaries.

Model: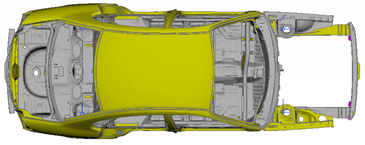

f=21.6Hz: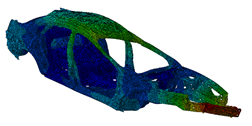

f=25.8Hz(must be maximized):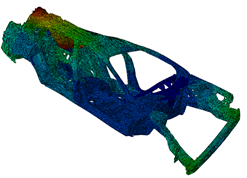



f=29.6Hz: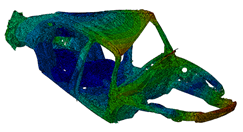

f=34.2Hz:

f=36.3Hz:

f=37.5Hz:

In the above figure, you can see the model and the first six modal eigenfrequencies.

Results

As shown in the next figure, the original mode 2 is now mode 4 maximizing the torsional eigenfrequency.

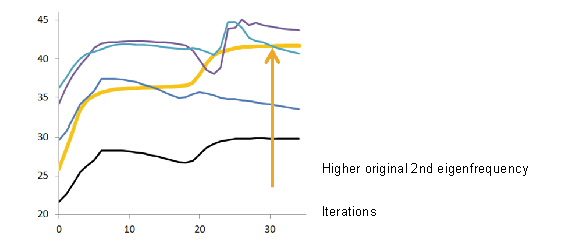When optimizing a specific eigenfrequency, the order of the eigenfrequencies might change during the optimization iterations.

Consequently, the eigenfrequencies might must be tracked during the optimization iterations.

The tracking is done using mode tracking as described in Mode Tracking.

By default, the modes are not tracked during the optimization. Mode tracking is activated in OPT_PARAM command:


DRESP
 ID_NAME  = 2nd_lowest_eigenfrequency
 DEF_TYPE = SYSTEM
 TYPE     = DYN_FREQ
 LC_SET   = MODAL, ALL, 2
END_

OBJ_FUNC
 ID_NAME = maximize_single_eigenfrequency
 DRESP   = 2nd_lowest_eigenfrequency
 TARGET  = MAX
END_

OPT_PARAM
 ID_NAME      = opt_params
 OPTIMIZE     = maximize_single_eigenfrequency
 MODETRACKING = ON
 MODENUMBERS  = 8
END_

For this example, at least 8 eigenfrequencies should be requested in the finite element input model defined by the user.