Maximization of the First Eigenfrequencies

It is important to consider more than the first natural eigenfrequency as illustrated in the above figure (b) when increasing the natural frequencies using optimization. At least, the next two first natural frequencies should be considered in the optimization.

All natural eigenfrequencies requested in the FE model are applied in the optimization if the ALL option is applied in the LC_SET parameter.

During the optimization, the various natural frequencies are automatically weighted by their distance from the lowest natural frequency, that is, when the other natural frequencies approach the first natural frequency during the optimization, the more they will be weighted. Generally, the first natural frequency is always maximized.

The design response is defined using the Kreisselmeier-Steinhauser formulation.

Any number of natural frequencies in the design response can be specified using the DRESP command.

Formulation of the Optimization Problem

The optimization task is to maximize the lowest modal eigenfrequencies with a volume constraint of 100%.


Model: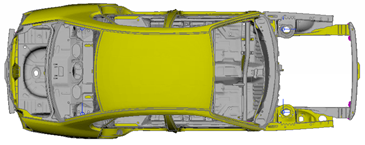
f=20.4Hz: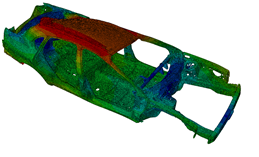
f=22.1Hz: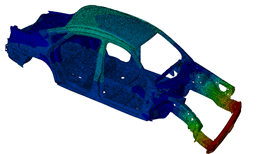
f=25.8Hz: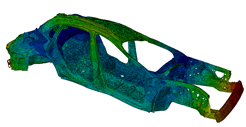
f=26.4Hz: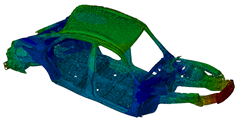
f=30.6Hz: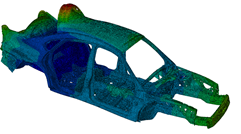
f=35.0Hz: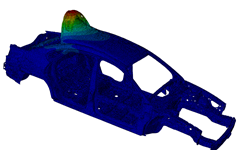

In the above figure, you can see the model and the first six modal eigenfrequencies.

Result and Convergence

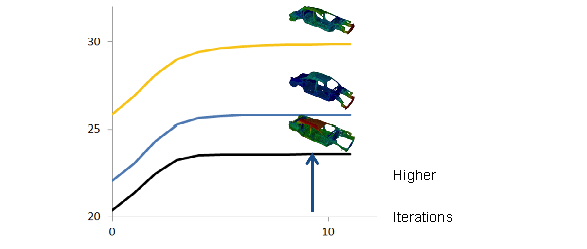
The following figure shows the objective function (maximize eigenfrequencies):

The constraint (Mass) is shown in the following figure:

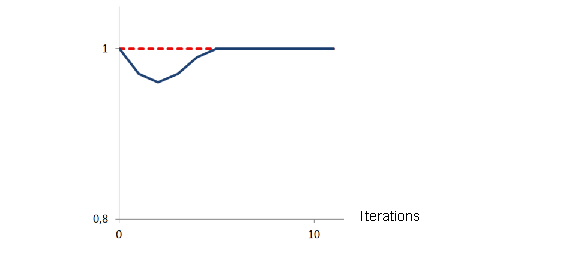The gradient of three eigenfrequencies over 15 iterations and the mass constraint are illustrated in the above figure. The constraint is fulfilled.

In this example, all calculated natural frequencies are considered for the objective function using the Kreisselmeier-Steinhauser formulation, and the definition is as follows:


DRESP
 ID_NAME  = all_lowest_eigenfrequencies
 DEF_TYPE = SYSTEM
 TYPE     = DYN_FREQ_KREISSEL
 LC_SET   = MODAL, ALL, ALL
END_

OBJ_FUNC
 ID_NAME = maximize_eigenfrequencies
 DRESP   = all_lowest_eigenfrequencies
 TARGET  = MAX
END_

If one has requested 10 eigenfrequencies in the finite element input model but only the first 5 eigenfrequencies are to be used in the optimization definition, then the design response for 5 eigenfrequencies is defined as follows:


DRESP
 ID_NAME  = all_lowest_eigenfrequencies_1_5
 DEF_TYPE = SYSTEM
 TYPE     = DYN_FREQ_KREISSEL
 LC_SET   = MODAL, ALL, 1-5
END_

OBJ_FUNC
 ID_NAME = maximize_eigenfrequencies_1_5
 DRESP   = all_lowest_eigenfrequencies_1_5
 TARGET  = MAX
END_