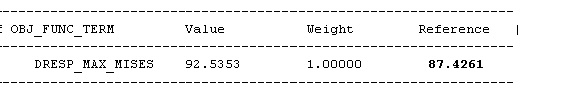Objective Function for Controller-Based Shape Optimization

Overview

The objective function is the function, which value can be maximized or minimized during the optimization. This function depends on the results of the FE analysis combined into design responses (DRESP).

Tosca Structure.shape works with a CONTROLLER-based algorithm that homogenizes the stresses with respect to a reference value. For simple optimizations this reference value can be ignored - Tosca Structure.shape will automatically generate a reference value that will be adequate for most cases.

Reference Stress

You might want to define a reference value yourself. In this case, you need to understand how Tosca Structure.shape works. The CONTROLLER-based algorithm is driven by following redesign rule:

Design nodes with stress above the reference value are moved outwards (growth).
Design nodes with stress below the reference value are moved inwards (shrinkage).

This produces components with homogenized stress in the design area.

So, if you choose a high reference value most design nodes will shrink to achieve this value. A low reference value has the opposite effect. With some practice, a good choice of reference value can be estimated giving the designer an optimal control over the shape optimization.

You can also choose the reference value to be a variable (for example, dependent on a design response). This has a special use for the design of relief notches where the reference value is chosen outside the design nodes area. This causes the design nodes to shrink until they have the same stress value as the reference value. This technique can only be done if the design area is relatively close to the area where the reference value is. Otherwise, you will not get the stress dampening effect of a relief notch.

Note:

A reference value is NOT the same as a CONSTRAINT. For most real structures, the maximum stress of a converged shape optimization will be some percent larger than the given or the automatically calculated reference stress.
Some structures and/or loading situations are not well suited for the CONTROLLER-based algorithm. You must have the correlation between growth in design nodes also minimizes the stresses.
- One example is a cantilever beam with a prescribed displacement at its free end. Due to the high stresses at the supports, the beam becomes thicker. Because of the prescribed displacement, the stresses are higher in the next iteration. The homogenization works, but the stresses increase because the beam stiffness increases as well.
- Another example is shape design in contact area: In this case, we know that the design rule must be the opposite the normal design rule because growth will cause even greater contact stresses. This can be turned around by using the optimization setting SCALE and set it to a negative value. Now, the shape optimization will shrink by high contact stresses and thus homogenize these to achieve a homogeneous contact.

Objective Function Terms

Tosca Structure.shape allows optimization on different stress hypotheses, strain formulations, and damage results. The most used equivalent stress is von Mises (SIG_MISES).


Solver-specific results	Description
ABQ_ND_PEEQ **	Abaqus PEEQ nodal value
Damage results	Description
DAMAGE DAMAGE_LC	Damage value from durability analysis Damage value from durability analysis with load case information (must use ONF 601)
Eigenfrequency results	Description
DYN_FREQ DYN_FREQ_KREISSEL	Eigenfrequency from modal analysis.
Stress hypotheses	Description
SIG_1 SIG_2 SIG_3	Maximum principal stress 2nd. principal stress Minimum principal stress
SIG_11 SIG_22 SIG_33 SIG_12 SIG_23 SIG_13	Components of stress tensor
SIG_ABS_123	Maximum of the absolute value of the principal stresses
SIG_ABS_3	Absolute value of the minimum principal stress
SIG_BELTRAMI SIG_DRUCKER_PRAGER SIG_KUHN SIG_MARIOTTE SIG_MISES SIG_SANDEL SIG_SAUTER SIG_TRESCA SIG_CONTACT_PRESSURE*	Beltrami stress hypothesis Drucker-Prager stress hypothesis Kuhn stress hypothesis Mariotte stress hypothesis von Mises stress hypothesis Sandel stress hypothesis Sauter stress hypothesis Tresca stress hypothesis Contact stress pressure
SIG_CONTACT_SHEAR * SIG_CONTACT_SHEAR_X * SIG_CONTACT_SHEAR_Y * SIG_CONTACT_TOTAL *	Total shear contact stress Shear X Contact stress Shear Y Contact stress Total Contact stress
Strain formulations	Description
STRAIN_ELASTIC* STRAIN_PLASTIC* STRAIN_TOTAL* STRAIN_ENERGY STRAIN_ENERGY_DENS	Elastic Strain Plastic Strain Total Strain (elastic + plastic) Strain energy Strain energy density
Analysis-independent results	Description
VOLUME WEIGHT	Volume design response Weight design response
* The marked design responses are supported only by the Abaqus and ANSYS® interface and only for nonlinear analysis. ** ABQ_ND_PEEQ is the scalar value that Abaqus calculates as PEEQ, which is NOT the same as STRAIN_PLASTIC. ABQ_ND_PEEQ is only available in Abaqus.

Important:

For controller-based shape optimization the reference value ( $φ_{i}^{r e f}$ ) has a special meaning. The reference value is the value around which Tosca Structure homogenizes the stress around. Thus, a value $φ_{i}^{r e f} = 0$ usually does not make sense and Tosca Structure calculates a default reference value if REFERENCE ( $φ_{i}^{r e f}$ ) is unset. The reference calculated can be seen in TOSCA.OUT:
Also, for controller-based shape optimization the user must either set all REFERENCE-values or none at all (automatic reference value calculation).

Differences in Objective Target Formulation

The objective formulation for the optimization varies depending on the objective target such as minimization/ maximization or a Min-Max/ Max-Min definition. For further details and formulas, see Minimization or Maximization of an Objective Function and Multidisciplinary Objectives (Minmax and Maxmin Formulations)