Mode Tracking

The mode tracking feature cannot be guaranteed to work properly for all examples due to the large material changes during topology optimization.

The modes of the different eigenfrequencies are compared in the modal assurance criterion (MAC) for identifying if the eigenfrequencies from optimization iteration to optimization iteration have been switching yielding:

${MAC}_{i,j}=\frac{{\left({\left\{\varphi \right\}}_i\right[Mass]{\left\{{\varphi }_{reference}\right\}}_j)}^2}{\left({\left\{\varphi \right\}}_i\right[Mass\left]{\left\{\varphi \right\}}_i\right)({\left\{{\varphi }_{reference}\right\}}_j\left[Mass]{\left\{{\varphi }_{reference}\right\}}_j\right)}$

where the initial modes are equal to the modes of the first iteration. Here, i are the reference modes and j modes in the optimization iteration. The modes in the first optimization iteration are used for identifying the eigenfrequencies through the optimization iterations.

The MAC matrix is equal to the unity matrix if the initial modes are equal to the modes in a given optimization iteration. However, this is only the case in the first optimization iteration due to the optimization changes. The largest components of the MAC matrix are determined in each optimization iteration for determining if any mode switching should be present. If significant off-diagonal terms exist in the MAC matrix, it indicates that the mode switching is present. The MAC matrix is printed in the TOSCA.OUT file. Then the user can see how close to 1 the components of the MAC matrix are and whether mode switching is present. If all the values in the MAC matrix are significantly below 1, it indicates that the applied mode set does not contain enough modes for mode tracking.

According to the above equation, mode tracking can lead to a significant increase in CPU-time. First, all modes of the eigenfrequencies must be cross-checked with each other. Sometimes a high number of cross-checks is required. Second, more eigenfrequencies must be calculated by the finite element solver.

During the optimization, the MAC Matrix can look like the following:

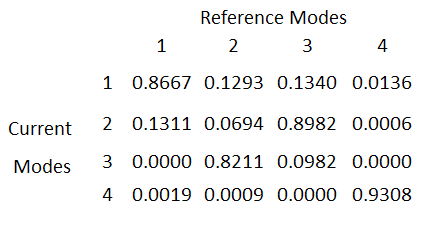
Mode tracking is defined in OPT_PARAM command as in the example below:

OPT_PARAM
 ID_NAME      = opt_params
 OPTIMIZE     = id_of_optimize
 MODETRACKING = ON
 MODENUMBERS  = 15
END_

Setting the command MODETRACKING equal to ON activates the mode tracking. Default for MODETRACKING is OFF. Consequently, mode tracking will only be applied if the user requests mode tracking.

The value of MODENUMBERS specifies how many eigenfrequencies should be used in the mode tracking. The default value of mode tracking is 5. In the above example, MODENUMBERS is set to 15 meaning that 15 eigenfrequencies will be used for the mode tracking. If, for example, one maximizes the first eigenfrequency, this eigenfrequency will be compared to the 15 specified eigenfrequencies in the MODETRACKING command. It is important that the modal analysis file specified by the user also leads to an analysis having the same or more eigenfrequencies than specified in the MODENUMBERS command. For this example, the user should specify at least 15 eigenfrequencies in the finite element file.

Sometimes it happens that many local modes having a low eigenfrequency appear during the optimization iterations. Normally, this will lead to high number for MODENUMBERS, which is not desirable because of high CPU-time. However, this can be partly circumvented by setting a number in the input finite element file avoiding the lower eigenfrequencies to be calculated. For example, if it is known that the initial eigenfrequency is around 200 Hz, then it should be specified in the finite element input file that the eigenfrequencies over 50 Hz only are to be calculated.

To improve the performance, it is additionally possible to restrict mode tracking to a certain group of nodes in the model (for example, every fifth node on the surface of the model) or nodes where lumped and rigid masses are attached. In this case, the node group is referenced in the MODETRACKING parameter as follows:

OPT_PARAM
 ID_NAME      = opt_params
 OPTIMIZE     = id_of_optimize
 MODETRACKING = ON, node_group
 MODENUMBERS  = 15
END_

When a node group is applied in the mode tracking, then the modal assurance criterion (MAC) yields:

${MAC}_{i,j}=\frac{{\left(\right|{\left\{\varphi \right\}}_i\left|\right|{\left\{{\varphi }_{reference}\right\}}_j|)}^2}{({\left\{\varphi \right\}}_i{\left\{\varphi \right\}}_i\left)\right({\left\{{\varphi }_{reference}\right\}}_j{\left\{{\varphi }_{reference}\right\}}_j)}$

where the modes are not scaled with the mass. Therefore, the nodes of the applied group are often chosen to be the nodes of frozen elements, lumped, or rigid masses.

Important: The finite element input file specified by the user should contain a modal analysis containing at least as many eigenfrequencies as the value of the MODENUMBERS parameter. A general rule for keeping the MODENUMBERS low and thereby saving CPU-time is to specify a lower bound for the calculated eigenfrequencies in the finite element file. Choosing 25% of the expected eigenfrequency as the lower bound usually suffices. For example, if the initial eigenfrequency of interest in the first optimization iteration is around 100 Hz, then it can be specified that only the eigenfrequencies over 25 Hz are to be calculated. The mode tracking feature cannot be guaranteed to work for all examples. Mode tracking is not recommended for the Kreisselmeier-Steinhauser formulation. Mode tracking can increase the CPU-time significantly for both the finite element solver and SIMULIA Tosca Structure. Restrict mode tracking to a smaller representative group of nodes to gain performance.