Optimize the Bending Plate Model

Define the Design Area (DV_SIZING):

DV_SIZING
 ID_NAME  = Opt_Plate_DESIGN_AREA_
 EL_GROUP = ALL_ELEMENTS
END_

To define the Objective Function, do the following:
1. Define a Design Response (DRESP) with the displacement in X-direction of the nodes on the right edge:
```
DRESP
 ID_NAME    = Disp_x
 LIST       = NO_LIST
 DEF_TYPE   = SYSTEM
 TYPE       = DISP_X_ABS
 ND_GROUP   = Z-LOAD
 GROUP_OPER = MAX
 LC_SET     = ALL, 1, ALL
END_
```
2. Reference the Design Response in the Objective Function (OBJ_FUNC) and set the TARGET to MINMAX:
```
OBJ_FUNC
 ID_NAME = Min_Disp_x
 DRESP   = Disp_x, 1.
 TARGET  = MINMAX
END_
```
  The maximum displacement out of the node set will be minimized.
To define the volume constraint, do the following:
1. Define a Design Response (DRESP) that contains the sum of the total volume of the optimization group:
```
DRESP
 ID_NAME    = Vol
 LIST       = NO_LIST
 DEF_TYPE   = SYSTEM
 TYPE       = VOLUME
 EL_GROUP   = ALL_ELEMENTS
 GROUP_OPER = SUM
END_
```
2. Reference the Design Response in a constraint (CONSTRAINT) and restrict it to 50% of the initial volume:
```
CONSTRAINT
 ID_NAME   = Max_Vol
 DRESP     = Vol
 MAGNITUDE = REL
 LE_VALUE  = 0.9
END_
```

Set up the optimization.

Define an element group (Cluster1, Cluster2,... [predefined in the example model]) for each of the clustering areas and assign them to a clustering design variable constraint as follows:

DVCON_SIZING
 ID_NAME    = CLUSTERING
 EL_GROUP   = Cluster1
 EL_GROUP   = Cluster2
 EL_GROUP   = Cluster3
 EL_GROUP   = Cluster4
 EL_GROUP   = Cluster5
 EL_GROUP   = Cluster6
 EL_GROUP   = Cluster7
 EL_GROUP   = Cluster8
 EL_GROUP   = Cluster9
 EL_GROUP   = Cluster10
 EL_GROUP   = Cluster11
 EL_GROUP   = Cluster12
 EL_GROUP   = Cluster13
 EL_GROUP   = Cluster14
 EL_GROUP   = Cluster15
 EL_GROUP   = Cluster16
 EL_GROUP   = Cluster17
 EL_GROUP   = Cluster18
 EL_GROUP   = Cluster19
 EL_GROUP   = Cluster20
 EL_GROUP   = Cluster21
 EL_GROUP   = Cluster22
 EL_GROUP   = Cluster23
 EL_GROUP   = Cluster24
 CHECK_TYPE = CLUSTER
END_

Reference the Design Variables, Objective Function, and constraints in the OPTIMIZE command:

OPTIMIZE
 ID_NAME    = Opt_Plate
 DV         = Opt_Plate_DESIGN_AREA_
 OBJ_FUNC   = Min_Disp_x
 CONSTRAINT = Max_Vol
 DVCON      = CLUSTERING
 STRATEGY   = SIZING_SENSITIVITY
END_

Define specific settings for optimization in the OPT_PARAM command:

OPT_PARAM
 ID_NAME                  = Bending_Plate_NL_OPT_PARAM_
 OPTIMIZE                 = Bending_Plate_NL
 AUTO_FROZEN              = LOAD
 THICKNESS_UPDATE         = CONSERVATIVE
 THICKNESS_MOVE           = 0.25
 STOP_CRITERION_LEVEL     = BOTH
 STOP_CRITERION_OBJ       = 0.001
 STOP_CRITERION_THICKNESS = 0.005
 STOP_CRITERION_ITER      = 4
END_

Important: Optimization with nonlinearities should run with THICKNESS_UPDATE = CONSERVATIVE to improve convergence.

Set an additional command in the OPTIONS command:
```
OPTIONS
 IGNORE_NUM_OF_OBJF_TERMS = YES
END_
```
This is needed because, by default, Tosca Structure allows only 50 terms in the objective definition. In this example, there are 79 nodes to be optimized. Thus, by ignoring the warning the optimization is allowed to run freely.
1. Optimum without considering nonlinear effects.
  
  Optimum when ignoring nonlinear effects contains members (at load application) with high thickness along the membrane in order to resist the displacement caused by the tension load (does not account for bending).
2. Optimum considering nonlinear effects.
  
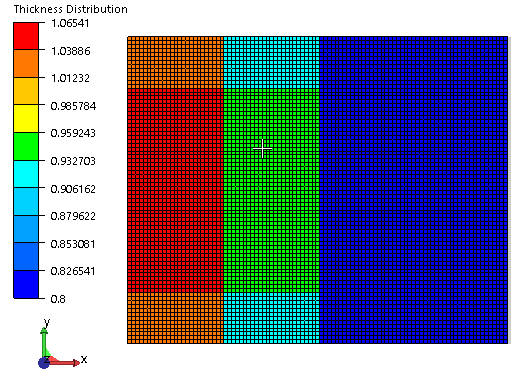
  Optimum when considering nonlinear effects results in a structure that resists the bending force (the load in the membrane is very minimal and, hence, not much contribution).