Plasticity corrections

Plasticity corrections provide an efficient method to evaluate the extent of plasticity in a structure based on a purely linear elastic solution. The method provides a substantial computational cost reduction compared to a full nonlinear elastic-plastic analysis, which is particularly valuable in optimization studies during the early design phase of a product or for concept design workflows.

Two types of plasticity correction are now available in Abaqus: Neuber and Glinka. Both methods apply a correction to the elastic results to capture the effects of local plasticity. The accuracy of the solution is generally quite good when the loading conditions lead to plastic deformation localized in small regions, such as in typical durability load cases. However, a full nonlinear analysis is recommended for loading conditions that lead to extended plastic deformation of the structure. In addition to the general static procedure, the Neuber and Glinka plasticity corrections are supported with the static linear perturbation procedure with multiple load cases, which can further substantially decrease the analysis time.

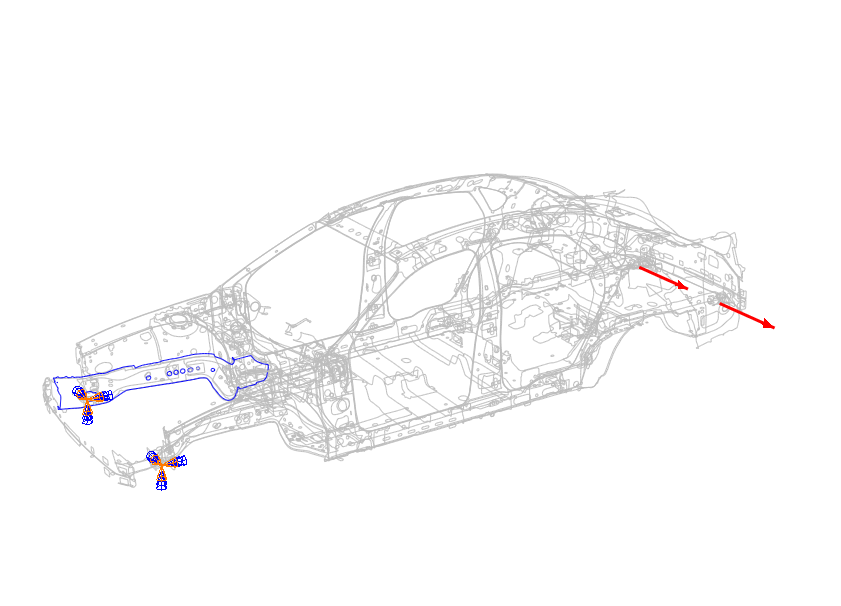
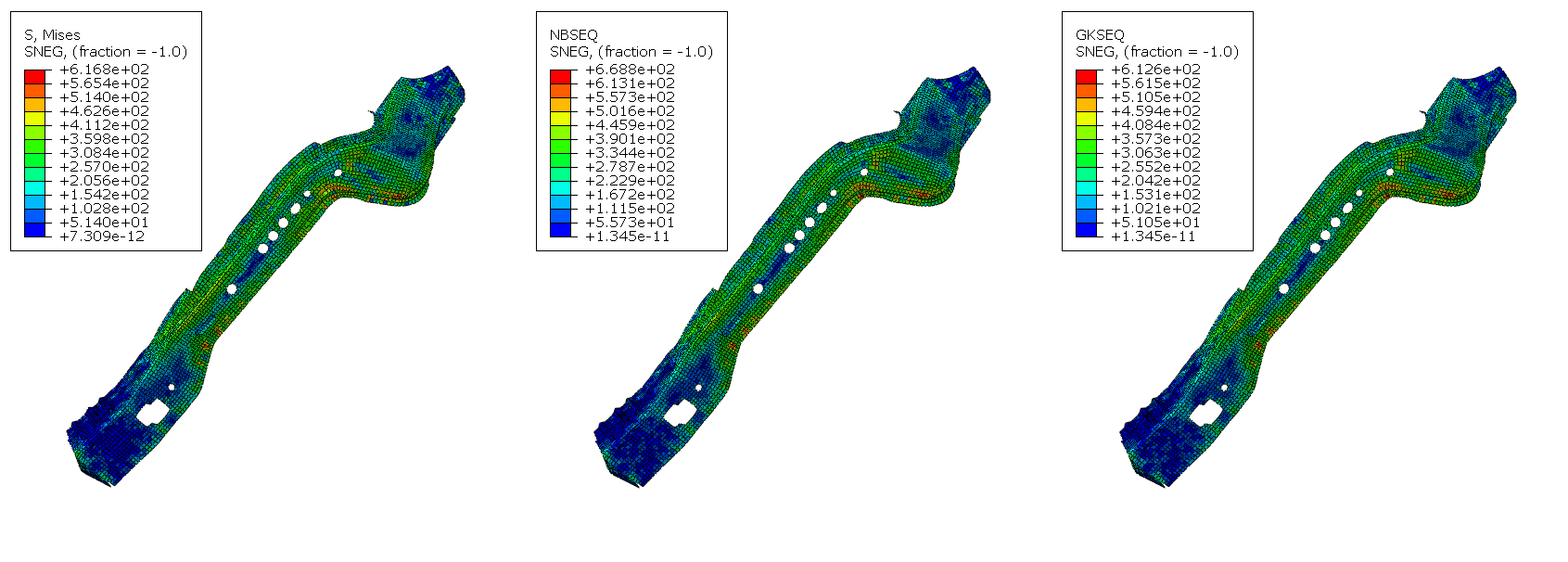
To illustrate the application of the method, consider a Body-in-White (BIW) model of a car subjected to the boundary conditions and loads shown in Figure 1 (courtesy of the Public Finite Element Model Archive of the National Crash Analysis Center at George Washington University). The stresses and plastic strains in the car body component highlighted in the figure are estimated using the Neuber and Glinka rules with a linear elastic analysis. The results are compared with those obtained from a full nonlinear elastic-plastic analysis. The stress and plastic strain results are presented in Figure 2 and Figure 3, respectively. The predictions based on plasticity corrections show good agreement with those obtained using a full elastic-plastic analysis, which is expected because plastic deformation is highly localized in small areas of the part. The Neuber's rule overestimates the equivalent stress and plastic strain, which is usually the case. As expected, the Glinka equivalent stress and plastic strain are lower than Neuber’s values. In this case, Glinka's rule slightly underestimates the elastic-plastic results.

Figure 1. Car model.

Figure 2. Comparison of elastic-plastic, Neuber, and Glinka stresses.

Figure 3. Comparison of elastic-plastic, Neuber, and Glinka plastic strains.