Contact mass scaling for Abaqus/Explicit

Abaqus/Explicit enforces contact using a penalty method. This approach tends to increase natural frequencies of the model and, in the absence of contact mass scaling, cause reductions in the stable time increment. For an analysis using the default contact penalty, this time reduction is usually around 5% or less, but it can become much more significant if the contact penalty stiffness is increased. Contact mass scaling artificially adds mass to surface nodes in contact, as needed, to avoid having contact stiffness influence the time increment size. The additional mass is removed when the surface nodes are no longer in contact.

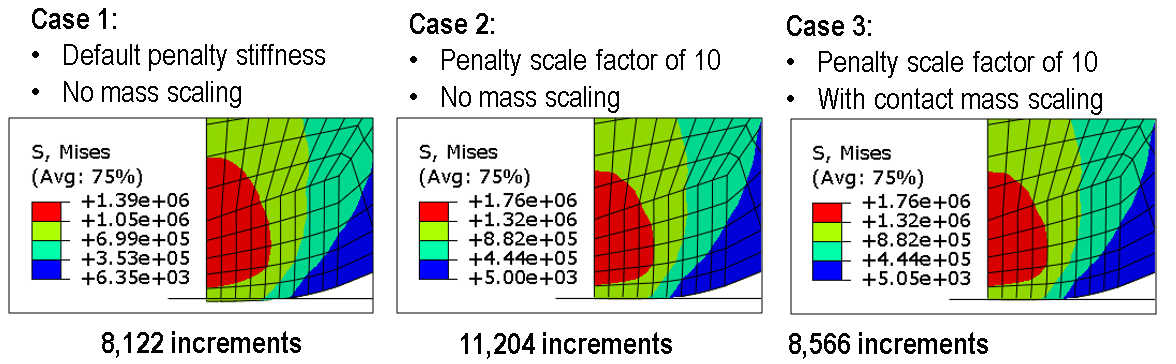
A classic Hertz contact example is shown in Figure 1. As explained in The Hertz contact problem, significant penetration is observed with the default penalty stiffness for Case 1 in Figure 1. Case 2 in Figure 1 has a penalty stiffness scale factor of 10 in effect. Case 2 provides an accurate solution but requires 38% more increments than Case 1. Case 3 in Figure 1 has contact mass scaling in effect along with a penalty stiffness scale factor of 10. The von Mises stress plots are in close agreement for Cases 2 and 3. Case 3 uses approximately 5% more increments than Case 1, which is related to greater (more accurate) compression of elements in Case 3 compared to Case 1.

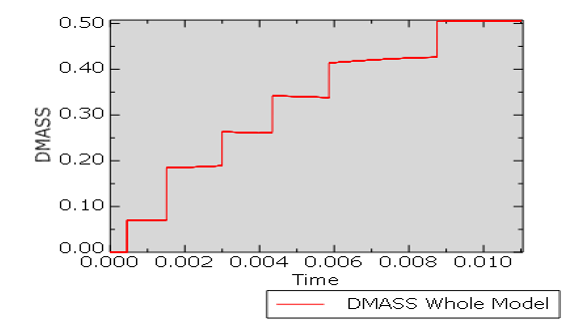
Figure 2 shows a history plot of output variable DMASS showing the percent change in total mass of the model over time. The “stair step” nature of the plot in Figure 2 reflects incremental changes in mass as additional surface nodes come into contact. At the end of the Case 3 simulation, the mass of the model is increased by 0.5% due to contact mass scaling.

New field and history output variables are available to support contact mass scaling:

• CNMSF (field output): Nodal contact mass scaling factor
• NDTTOTAL (field output): Stable time increment over contact surfaces with effects of element and contact mass scaling
• CDMASS (history output): Percent change in mass of the model due to contact mass scaling

In addition, output variables DMASS and ALLMW are enhanced to include the effects of contact mass scaling.

Figure 1. Hertz model.

Figure 2. Percentage variation of mass during the analysis.